Uživatelské nástroje
Postranní lišta
 Přidat stránku do knihy
Přidat stránku do knihy  Odebrat stránku z knihy
Odebrat stránku z knihy Toto je starší verze dokumentu!
Obsah
Třídění/Řazení a vyhledávací algoritmy
Třídění vs řazení
Třídění je uspořádání objektů podle podobných vlastností. Způsob třídění je vždy závislý na oboru, který s těmito objekty pracuje.
Řazení je způsob uspořádání objektů do specifikovaného pořadí. Řazení může být provozováno podle různých kritérií (abecedně, vzestupně, sestupně).
Tyto dva pojmy bývají často zaměňovány.
Složitost algoritmů
Složitost algoritmů (někdy taky asymptotická složitost) je funkce, která vyjadřuje počet elementárních kroků v závislosti na vstupních datech dané funkce. Značí se O.
Rozdíl mezi jednotlivými třídami složitosti se dá jednoduše pochopit na těchto dvou příkladech. Když máme první algoritmus se složitostí O(n) a druhý algoritmus se složitostí O(2n) stačí nám ten druhý spustit na dvakrát rychlejším stroji a rozdíl je smazán. Pokud však máme první algoritmus se složitostí O(n) a algoritmus se složitostí O(n2) bude při různé velikosti stoupat náročnost v závislosti na n 10x, 20x,…
Třídící algoritmy
Bubble sort
Princip:
- Dostanu zadané pole.
- Procházím pole, pokud je prvek vlevo menší než prvek vpravo prohodím je
- Opakuji dokud není pole seřazeno od největšího po nejmenší (zprava doleva)
Složitost: O(n2) → za každý prvek pole projdu pole dvakrát
Ukázka algoritmu:
function bubbleSort(array) { for (var i = 0; i < array.length - 1; i++) { for (var j = 0; j < array.length - 1 - i; j++) { if (array[j] < array[j + 1]) { var tmp = array[j]; array[j] = array[j + 1]; array[j + 1] = tmp; } } } }
Insert sort
Princip:
- Dostanu pole
- Procházím pole zleva doprava a vždy každý prvek zařadím na místo podle velikosti
- Dostávám pole seřazené zleva doprava od největšího po nejmenší
Složitost: Složitost je O(n2), ale při téměř seřazeném poli se blíží O(n)
Ukázka algoritmu:
function insertSort(array) { var stepCounter = 0; for (var i = 0; i < array.length - 1; i++) { var j = i + 1; var tmp = array[j]; while (j > 0 && tmp > array[j - 1]) { array[j] = array[j - 1]; j--; array[j] = tmp; } } }
Merge sort
Princip:
- Dostaneme pole
- Toto pole si rozdělíme na dvě podpole
- Dokud není pole rozděleno na jednoprvkové pole opakuj krok č.2
- Jakmile máme jednoprvková pole spojíme je dohromady tak, aby byly seřazeny
- Jakmile máme jenom dvě podmnožiny porovnáme vždy jednotlivé prvky množiny a vždy ten větší přidáme do finálního pole –> postupujeme až máme ve finálním poli prvky od největšího po nejmenší
Složitost: Složitost algoritmu O(n * log(n))
Protože to nejsem schopný naprogramovat ukázku máte zde ![]() .
.
Quick sort
Princip:
- Dostaneme pole
- Zvolíme si jeden prvek pole (pivot) a rozdělíme zbytek pole na prvky větší než pivot a na prvky menší než pivot
- Pivota umístíme mezi tyto dvě množiny → pivot je na místě, kam by patřil v seřazeném poli
- Kroky opakujeme, dokud nemáme všechny prvky seřazeny
Složitost: Složitost u quick sortu je hodně závislá na volbě pivota(resp. pivotů). Pokud je pivot mediánem hodnot může být složitost O(n * log(n)), pokud však je pivot největším nebo nejmenším prvkem pole je složitost O(n2). Pivota můžeme vybrat, jako fixní pozici v tabulce (např. vždy poslední nebo první nebo prostřední prvek) nebo, což se považuje za idealnější případ, se vyberou tři hodnoty a z nich se udělá medián.
Protože to nejsem schopný naprogramovat ukázku máte zde ![]() .
.
Selection sort
Princip:
- Dostaneme pole
- Vyhledáme největší prvek pole a umístíme ho doleva
- Toto opakujeme, dokud nemáme seřazeno
Složitost: Složitost je sice u selection sortu vysoká O(n2), ale dobrá je u něj jeho nízká paměťová náročnost
Vyhledávací algoritmy
Lineární hledání (také sekvenční hledání)
Princip: Procházím všechny prvky, dokud nenajdu ten hledaný.
Složitost: O(n)
Binární hledání (též metoda půlení intervalů)
Princip:
- Pole ve kterém se dá použít půlení intervalů musí být seřazeno (v tomto případě od největšího po nejmenší)
- Podívám se na prostřední prvek pole
- Pokud je můj hledaný prvek větší opakuji to stejné vpravo, pokud menší tak vlevo
- Opakuji dokud nenajdu hledané číslo
Složitost: O(log2(n))
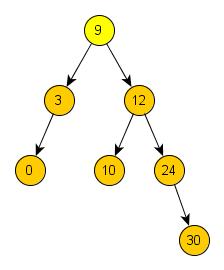
Metoda binárního vyhledávacího stromu
Princip: Tvořím binární strom (viz. obrázek) tak, že vždy v levé větvi jsou menší prvky a v pravé jsou větší prvky. Hledaný prvek hledáme tak, že za ním jdeme po větvi.
Složitost: V závislosti na vyvážení stromu (= vyvážený počet větví obou stranách) může být buď O(log(n)) pro vyážený strom nebo O(n) pro nevyvážený.

 Zobrazit/upravit knihu (
Zobrazit/upravit knihu ( Nápověda
Nápověda